【大学受験】教えてもらったかもしれない対数の概念

理系学生は普通対数が使える

　3/1の就活解禁日から、卒業生たちがわんさか訪れています。昨日は鉄鋼大手入社1年目のK君がやってきて、「ブログ読んでます！」と言っていたので登場させてみましょうか。工場見学の際に、「スーツは着なくてもいいけど、ジーンズでは来ないで。」と言ったら、なんとジャージで登場！！修士論文発表会では、「関係各位に感謝します。」と言って終わるところを「関係各位に陳謝します。」と言い間違え、全部持っていっちゃいました。不器用なんですけど、なんとも憎めないとてもいい性格をしている彼は、職場に人たちから可愛がってもらっているようです。このままでいて欲しいような、でもそれではマズいような複雑な心境です。

　本日は対数の話題。先日、工学研究科長の講演を聞く機会がありました。「モデル化をしたり解析をしたりするときには、とりあえず対数を使ってみるといい。だいたい何にでも使えて便利だった。」と。そう、普通のグラフ用紙を使ってグラフを描いても見ただけでは次数がわからないので、私たちは対数グラフを使います。軸の一方だけが対数になっている片対数（セミログ）グラフや、両軸ともに対数になっている両対数（ログログ）グラフにプロットして、傾きや切片から未知パラメーターを求めることがしばしばあります。というわけで、理系に進む人は面倒でもちゃんとやっておいてください。

対数なんか忘れてしまった人のためにちょっと復習

　数Ⅱで習うものなので、文系の人も一度は勉強しているはずですけど復習です。たとえば、2を3回かけると8になります。これが対数変換するとこんな形に変わります。

f:id:gajumarun:20190309214024j:plain

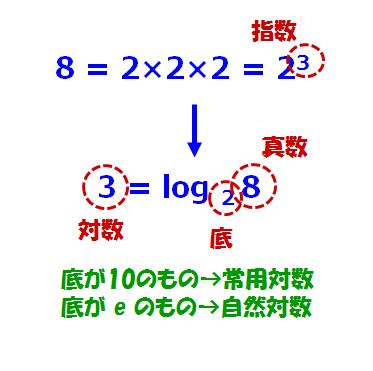
2を何乗すると8になるかの何乗のところを対数と呼びます。上の式では「指数」と呼んで、下の式では「対数」と呼びます。ややこしいですね。2のことを「底（てい）」といいますが、底が10のものが常用対数、eのものが自然対数です。

　小さい値の差は大きく、大きい値の差は小さく表すことができる便利な方法なので、意外と日常生活でも使われています。

f:id:gajumarun:20190309213942j:plain

身近で使われる対数

　マグニチュードは対数です。マグニチュードは地震そのものの規模を示すもので、マグニチュードをM、地震が発するエネルギーの大きさをE [J]とすると、

　log₁₀E = 4.8 + 1.5M

で表すことができます。ということは、Mが1大きくなるとlog₁₀Eが1.5大きくなります。10^1.5 ＝約31.6です。Mが2大きくなると、10^1.5^ｘ2 = 10³ = 1000 倍になります。マグニチュード5と7ではエネルギーが1000倍も違うのです。ちなみに、震度は揺れの大きさを表し、マグニチュードと震源からの距離が関係します。

　酸性の度合いを示すpHも対数です。溶液中の水素イオン濃度をpH = －log [H⁺]で表すため、数字が小さい方が酸性度が強いことになります。普通は「pH5の炭酸水を飲もうか。」なんて使わないですね。pH 10の強アルカリ性の温泉に研究室旅行で行くときには、pH試験紙持っていきましたけど、これも普通じゃないですね。身近じゃないか。

　音の大きさを表すdb（デシベル）とか、何等星と星の明るさを表す等級も対数です。0デシベルの電圧10倍が20デシベル、100倍が40デシベルと20デシベルごとに10倍になるしくみです。0デシベルは人の聴力の限界、20デシベルは葉が触れる音、40デシベルは図書館、60デシベルは普通の会話、80デシベルは電車の中の音といわれています。星の明るさでは、１等級が100^0.2に相当するので、1等星は6等星の100倍の明るさです。